Head Weight
April 22, 2006 5:41 PM Subscribe
How can I measure the weight of my head without cutting it off?
It's really important.
It's really important.
p.s. In step 2., you should be filling the measuring receptacle with water, not your friend.
posted by dersins at 5:57 PM on April 22, 2006
posted by dersins at 5:57 PM on April 22, 2006
Seems to me the obvious way is: lie on your back with your shoulders on the floor and your head relaxed on a scale. Get a friend to read the scale.
posted by Eater at 5:59 PM on April 22, 2006
posted by Eater at 5:59 PM on April 22, 2006
Odinsdream, the mass of displaced water is equal to the mass of the object displacing it.
Water has a density of 1 gram per cubic centimeter. Thus, the volume of displaced water in cubic centimeter should be equal in number to the mass of the displacing object in grams.
Or so I remember.
posted by dersins at 6:00 PM on April 22, 2006
Water has a density of 1 gram per cubic centimeter. Thus, the volume of displaced water in cubic centimeter should be equal in number to the mass of the displacing object in grams.
Or so I remember.
posted by dersins at 6:00 PM on April 22, 2006
Lie down and place just your head on a scale? A kitchen scale might work better because it measures in smaller increments than a typical "bathroom scale" type of scale.
posted by boomchicka at 6:00 PM on April 22, 2006
posted by boomchicka at 6:00 PM on April 22, 2006
options
more
huh, I never realized how difficult the problem is. I'm not sure if any of those would work.
dersins, that gives your head's volume. You'd need to know your head's density to figure out the mass from that. (A avg. head's density is approximately 1050kg/m^3, apparently.)
posted by neda at 6:00 PM on April 22, 2006
more
huh, I never realized how difficult the problem is. I'm not sure if any of those would work.
dersins, that gives your head's volume. You'd need to know your head's density to figure out the mass from that. (A avg. head's density is approximately 1050kg/m^3, apparently.)
posted by neda at 6:00 PM on April 22, 2006
Or, what Eater said.
posted by boomchicka at 6:00 PM on April 22, 2006
posted by boomchicka at 6:00 PM on April 22, 2006
To expand on dersin's comment:
(1) Plunge your head into a tub, mouth closed and puckered to get rid of as much air as possible, and measure the water displacement to obtain your head volume.
(2) Subtract out the volume of bone (the bone material only, not the enclosed space). An average skull is 1.0 kg and 1810 kg/m^3, and that ought to be pretty close.
(3) The remaining volume can be converted to mass by using the rough value of 1070 kg/m^3 for human tissue (surprisingly most tissue is pretty similar, reference). Add that to the 1.0 kg skull weight and you should have the head weight to maybe within 10 or 20 percent.
posted by rolypolyman at 6:01 PM on April 22, 2006
(1) Plunge your head into a tub, mouth closed and puckered to get rid of as much air as possible, and measure the water displacement to obtain your head volume.
(2) Subtract out the volume of bone (the bone material only, not the enclosed space). An average skull is 1.0 kg and 1810 kg/m^3, and that ought to be pretty close.
(3) The remaining volume can be converted to mass by using the rough value of 1070 kg/m^3 for human tissue (surprisingly most tissue is pretty similar, reference). Add that to the 1.0 kg skull weight and you should have the head weight to maybe within 10 or 20 percent.
posted by rolypolyman at 6:01 PM on April 22, 2006
The mass of displaced water is equal to the mass of the object displacing it? So 1cc of lead displaces more water than 1cc of plastic?
posted by Eater at 6:02 PM on April 22, 2006
posted by Eater at 6:02 PM on April 22, 2006
But I probably remember wrong. It's been a damn long time.
posted by dersins at 6:03 PM on April 22, 2006
posted by dersins at 6:03 PM on April 22, 2006
I think you're mixing up mass & weight. The masses aren't equal. If an object is floating, there's no net Force, and it's weight (the downward vertical force on the object) is equal to the weight of the water displaced (which is the buoyant force--the upward vertical force on the object).
so object weight= F(buoyant)
mg=pVg (p=density of fluid, V=volume of fluid displaced, m=mass of object)
posted by neda at 6:09 PM on April 22, 2006
so object weight= F(buoyant)
mg=pVg (p=density of fluid, V=volume of fluid displaced, m=mass of object)
posted by neda at 6:09 PM on April 22, 2006
Hmm. I am still thinking about this...No, dersin's solution doesnt work. That relies on buoyancy - i.e. things floating of their own accord. So forget that.
I am trying to work out a solution that relies on getting on a spinning wheel (like at a playground) along with some angular momentum calculations but I'm not sure its right yet...
posted by vacapinta at 6:09 PM on April 22, 2006
I am trying to work out a solution that relies on getting on a spinning wheel (like at a playground) along with some angular momentum calculations but I'm not sure its right yet...
posted by vacapinta at 6:09 PM on April 22, 2006
Easy! Find your total weight, and just subtract out the weight of your limbs and torso.
I would approximate it by measuring the volume of your head (via dunking - don't forget those sinuses!) and the volume of your whole body (Archimedes style), measure the weight of your whole body, do some division, and Eureka! Run around the city naked yelling roughly how much your head weighs!
Grey matter's less dense than muscle, plus we all know you didn't really fill your sinuses with water, so knock off a couple pounds if you want to feel better about yourself.
BTW: The displacing an equal mass trick is only true for objects that are FLOATING.
posted by aubilenon at 6:12 PM on April 22, 2006
I would approximate it by measuring the volume of your head (via dunking - don't forget those sinuses!) and the volume of your whole body (Archimedes style), measure the weight of your whole body, do some division, and Eureka! Run around the city naked yelling roughly how much your head weighs!
Grey matter's less dense than muscle, plus we all know you didn't really fill your sinuses with water, so knock off a couple pounds if you want to feel better about yourself.
BTW: The displacing an equal mass trick is only true for objects that are FLOATING.
posted by aubilenon at 6:12 PM on April 22, 2006
Best answer: Yeah, I'm remembering my physics all wrong. I think the solution probably involves being hung by your heels from a spring-scale with your head in a vat of liquefied heads to achieve neutral head buoyancy, and then subtracting the reading on the spring-scale from the known weight of your entire body.
posted by dersins at 6:18 PM on April 22, 2006 [24 favorites]
posted by dersins at 6:18 PM on April 22, 2006 [24 favorites]
Remember Archimedies, kids, and the Golden Crown. How could the king know that the crown was pure gold?
The other problem is, of course, define "head" -- how much of the neck counts?
Lying with your head on a scale would get you a reasonable close number.
posted by eriko at 6:25 PM on April 22, 2006 [1 favorite]
The solution which occurred when he stepped into his bath and caused it to overflow was to put a weight of gold equal to the crown, and known to be pure, into a bowl which was filled with water to the brim. Then the gold would be removed and the king’s crown put in, in its place. An alloy of lighter silver would increase the bulk of the crown and cause the bowl to overflow.So, yes, you need to know the aggregate density of your head for this to work. If you knew that, you could get a substance of similar density, dunk your head, measure the displace water, then refill, drop in bits of stuff until you displaced the same amount of water, then weigh the bits you dropped in. Complicated, to be sure.
The other problem is, of course, define "head" -- how much of the neck counts?
Lying with your head on a scale would get you a reasonable close number.
posted by eriko at 6:25 PM on April 22, 2006 [1 favorite]
Can I piggyback? I am interested in measuring the weight (not volume) of some mammary glands to which I am rather attached.
posted by booksandlibretti at 6:31 PM on April 22, 2006
posted by booksandlibretti at 6:31 PM on April 22, 2006
vacapinta - if you're thinking what i think you're thinking (scanning the rotation axis along the body) that's pretty damn sweet.
posted by andrew cooke at 6:31 PM on April 22, 2006
posted by andrew cooke at 6:31 PM on April 22, 2006
Oh, dear, dersins. The phrase "vat of liquefied heads" made me laugh until I couldn't breathe. Thanks a lot.
posted by Faint of Butt at 6:32 PM on April 22, 2006
posted by Faint of Butt at 6:32 PM on April 22, 2006
Dammit. In my attempt to be SFW, I wind up looking like an idiot. I am interested in measuring the whole thing, not just the gland.
posted by booksandlibretti at 6:33 PM on April 22, 2006
posted by booksandlibretti at 6:33 PM on April 22, 2006
booksandlibretti - in that case the best approach is to guess the elasticity and density and then numerically model the system. you should be able to find the relationship between the mass and the driving frequency necessary for simple harmonic motion.
then it's just a case of measuring the resonant frequency experimentally....
posted by andrew cooke at 6:43 PM on April 22, 2006 [1 favorite]
then it's just a case of measuring the resonant frequency experimentally....
posted by andrew cooke at 6:43 PM on April 22, 2006 [1 favorite]
Well, the most accurate way other than cutting off your head would be the following:
1) Weigh yourself
2) Cut off your body
3) Subtract weight of body from initial measurements.
4) Compare to friends to see who really is the smartest.
posted by allen.spaulding at 6:48 PM on April 22, 2006
1) Weigh yourself
2) Cut off your body
3) Subtract weight of body from initial measurements.
4) Compare to friends to see who really is the smartest.
posted by allen.spaulding at 6:48 PM on April 22, 2006
A variant of dersins' answer, with a second bucket in place of an accomplice:
Place bucket A (large enough to contain your head) inside bucket B (of at least twice the volume). Fill bucket A with water to the very brim. Hold bucket A down, plunge your head into bucket A, and remove it. Remove bucket A from bucket B without spilling water. Weigh bucket B, dump out the water, and subtract the weight of empty bucket B.
The answer is what your head would weigh if its density were exactly that of water. I think this is a very reasonable approximation. What error are you willing to tolerate in your measurement? (Before you say "none" you must say exactly where your head ends and your neck begins.)
You must hold bucket A down when doing this, or else it will float in the water displaced into bucket B, and possibly spill.
posted by Aknaton at 6:49 PM on April 22, 2006
Place bucket A (large enough to contain your head) inside bucket B (of at least twice the volume). Fill bucket A with water to the very brim. Hold bucket A down, plunge your head into bucket A, and remove it. Remove bucket A from bucket B without spilling water. Weigh bucket B, dump out the water, and subtract the weight of empty bucket B.
The answer is what your head would weigh if its density were exactly that of water. I think this is a very reasonable approximation. What error are you willing to tolerate in your measurement? (Before you say "none" you must say exactly where your head ends and your neck begins.)
You must hold bucket A down when doing this, or else it will float in the water displaced into bucket B, and possibly spill.
posted by Aknaton at 6:49 PM on April 22, 2006
lay on the floor with the bathroom scale under your head
really, guys, this isn't that hard ...
posted by pyramid termite at 6:54 PM on April 22, 2006
really, guys, this isn't that hard ...
posted by pyramid termite at 6:54 PM on April 22, 2006
Just find someone with a head about the same size as yours and cut theirs off. Should give you a pretty good idea. To be on the safe side, you may want to do this five or more times and take the average.
Or you could do the whole volume-density thing suggested above, but that seems like a lot of work. (And math is hard)
posted by quin at 6:56 PM on April 22, 2006
Or you could do the whole volume-density thing suggested above, but that seems like a lot of work. (And math is hard)
posted by quin at 6:56 PM on April 22, 2006
I too am curious about what accuracy you need here.
It looks like you might be able to feed yourself through an MRI machine and guesstimate a fairly good result. It would basically be a variation on the "average head density" approaches above, but subdividing into "average bone density", "average brain density" etc etc for a more accurate result.
posted by Leon at 7:07 PM on April 22, 2006
It looks like you might be able to feed yourself through an MRI machine and guesstimate a fairly good result. It would basically be a variation on the "average head density" approaches above, but subdividing into "average bone density", "average brain density" etc etc for a more accurate result.
posted by Leon at 7:07 PM on April 22, 2006
PleasePleasePleasePlease tell me why you want to know!
posted by radioamy at 7:08 PM on April 22, 2006
posted by radioamy at 7:08 PM on April 22, 2006
You could measure the volume of your head as described above, then measure the volume of your entire body by doing the same thing in a bathtub. If your body has a roughly uniform density, which is a not-obviously-invalid assumption, the ratio of the volume of your head to the volume of your entire body including your head ought to be the same as the ratio of the weight of your head to that of your entire body.
posted by cerebus19 at 7:34 PM on April 22, 2006
posted by cerebus19 at 7:34 PM on April 22, 2006
I can think of one very accurate way:
Choose a liquid which will cause you to float exactly at the top of your head. Since you are floating, the mass of water you are displacing is equal to the mass of your body.
Define a neck-line to be wherever the "head" ends and the body begins in your experiment.
Have someone lift you so that you are now floating at the neck line. The amount of force required to keep you at this point is the weight of your head.
posted by clord at 8:22 PM on April 22, 2006
Choose a liquid which will cause you to float exactly at the top of your head. Since you are floating, the mass of water you are displacing is equal to the mass of your body.
Define a neck-line to be wherever the "head" ends and the body begins in your experiment.
Have someone lift you so that you are now floating at the neck line. The amount of force required to keep you at this point is the weight of your head.
posted by clord at 8:22 PM on April 22, 2006
Why hasn't anyone suggested just looking in a medical textbook for the average weight of a human head?
I think all these answers that involve displacement or dunking the head are on the wrong track. All that can possibly tell you is the volume, not the mass or weight of the head. Volume requires a measure of density to convert into weight, and so all you've really done is turn one unanswerable question ("How much does my head weigh?") into another unanswerable question ("What is the average density of my head?").
Also implicit in this question is what is the precise definition of "a head"? Are you including part of the spine? Neck? Where does the cutoff occur? Right at the base of the skull? Midpoint of the neck?
posted by Rhomboid at 8:44 PM on April 22, 2006
I think all these answers that involve displacement or dunking the head are on the wrong track. All that can possibly tell you is the volume, not the mass or weight of the head. Volume requires a measure of density to convert into weight, and so all you've really done is turn one unanswerable question ("How much does my head weigh?") into another unanswerable question ("What is the average density of my head?").
Also implicit in this question is what is the precise definition of "a head"? Are you including part of the spine? Neck? Where does the cutoff occur? Right at the base of the skull? Midpoint of the neck?
posted by Rhomboid at 8:44 PM on April 22, 2006
Have someone lift you so that you are now floating at the neck line. The amount of force required to keep you at this point is the weight of your head.clord, I don't think that will work. The weight of the object acts on the entire object, so you can't just say that because the head is above water it is not contributing to its buyancy.
Here's a mental experiment to prove that is not how it works. Take two identical hourglass-shaped vessels. Fill half of each with lead and leave the other half filled with air. Clearly, one end will be much more dense than the other. Now put these two vessels in tubes (so that they stand endwise) and fill the tubes with water. Except put one with the lead end down and one with the air end down. If your theory is correct then they should float at different levels, because otherwise the part floating above the water (analogous to the head in your experiment) has different masses. I say they will always float at the same level because they have identical masses and identical volumes. This proves that your experiment is measuring the volume, not mass, of the part of the body that you expose by pulling it up out of the water.
posted by Rhomboid at 8:52 PM on April 22, 2006
"Is that a cardigan you're wearing?"
"No, it's a Hedway."
"What's a Hedway?"
"About 8 pounds."
See, that's why he wants to know. To get the correct number for the punchline.
posted by The Deej at 8:58 PM on April 22, 2006
"No, it's a Hedway."
"What's a Hedway?"
"About 8 pounds."
See, that's why he wants to know. To get the correct number for the punchline.
posted by The Deej at 8:58 PM on April 22, 2006
Just to restate my last comment.... clord posits that the force required to pull an object up out of the water is proportional to the mass that is exposed. I posit that this is not the case. Imagine taking two of the described hourglass-shaped devices. You put them in water, and then pull them up above the surface with a scale, measuring force and displacement along the way. These two vessels have the same mass and volume, but it is distributed differently since one is lead-down. I contend that the force-displacement you will record on the scale for pulling them up will be identical. But the amount of mass exposed differs since one will be coming up air-first and the other lead-first. Thus, you cannot use this to measure the mass of the portion removed from the water, only the volume. This is essentially just a pure restatement of the "dunk your head to find the volume" scenario, which does nothing to actually give you the weight/mass of the head.
posted by Rhomboid at 9:02 PM on April 22, 2006
posted by Rhomboid at 9:02 PM on April 22, 2006
Don't forget that your head has several holes in it, which are normally full of air. This will be a factor if you're trying to determine the volume and density of your head -- unless, of course, you plan to compact your head before measuring. But that, too, will affect density.
posted by Acetylene at 9:28 PM on April 22, 2006
posted by Acetylene at 9:28 PM on April 22, 2006
Best answer: Underwater weighing as aubilenon mentioned.
The density is very close to 1 for all flesh. You can verify this yourself based on the fact that some people float in water, some sink, some people can turn it on and off by holding their breath. At least in my experience, my head seems pretty close to that floating mark too, i.e., I don't feel like i'm tipping towards or away my head when I float on my back. I know it's approximate, but any solution will be.
Determine your volume by displacement. Let this equal A. Determine your nonhead volume by displacement. Let this equal B. Determine your underwater mass. Let this equal C. Determine your mass with all but your head submerged. Let this equal D. So we have:
A: Body volume
B: Nonhead body volume
C: Hydrostatic mass
D: Head-above-water hydrostatic mass
We use the approximation that your overall hydrostatic density can be used to correct for your nonhead mass. This is probably the best approximation because it includes the vast majority (>90%) of your mass, and individual variations in mass are likely due to abdominal fat deposits.
So we introduce an overall hydrostatic density:
C/A
This is your effective density in water. It will be very close to zero. If it is less than zero, you will float. This makes things trickier but not impossible (use an upside down spring scale).
We have your nonhead volume, B, and your overall hydrostatic density, to determine your nonhead hydrostatic mass:
B*(C/A).
Your head-above water measurement will include the in-air mass of your head, and the nonhead hydrostatic mass. So the mass of your head is
M=D-B*(C/A)
The B*(C/A) term will be very, very close to zero. You can probably get a good approximation from just D. Don't forget to exhale maximally when you take hydrostatic measurements. Typically in body density measurements it's done just to ensure a true density is calculated (a correction factor for intestinal gases is included, too), but for our purposes, you just need to be consistent, since we don't care about your true hydrostatic mass -- we're just using it as a correction factor.
As an aside, you will get an estimate of your body fat percentage. Typical underwater weighing measurement assume fat has a density of ca .9, and fat free mass has a density of ca 1.1. So your body fat percentage is (495/True density) - 450, or (457/True density) - 414.2, depending whom you trust. These are known as the Siri and Brozek equations. The disclaimers above about dead volume in lungs and the GI apply moreso here; body fat determination is extremely error-prone, especially in those <1 0 and>30% BF (most of us...).
posted by oxonium at 9:43 PM on April 22, 2006
The density is very close to 1 for all flesh. You can verify this yourself based on the fact that some people float in water, some sink, some people can turn it on and off by holding their breath. At least in my experience, my head seems pretty close to that floating mark too, i.e., I don't feel like i'm tipping towards or away my head when I float on my back. I know it's approximate, but any solution will be.
Determine your volume by displacement. Let this equal A. Determine your nonhead volume by displacement. Let this equal B. Determine your underwater mass. Let this equal C. Determine your mass with all but your head submerged. Let this equal D. So we have:
A: Body volume
B: Nonhead body volume
C: Hydrostatic mass
D: Head-above-water hydrostatic mass
We use the approximation that your overall hydrostatic density can be used to correct for your nonhead mass. This is probably the best approximation because it includes the vast majority (>90%) of your mass, and individual variations in mass are likely due to abdominal fat deposits.
So we introduce an overall hydrostatic density:
C/A
This is your effective density in water. It will be very close to zero. If it is less than zero, you will float. This makes things trickier but not impossible (use an upside down spring scale).
We have your nonhead volume, B, and your overall hydrostatic density, to determine your nonhead hydrostatic mass:
B*(C/A).
Your head-above water measurement will include the in-air mass of your head, and the nonhead hydrostatic mass. So the mass of your head is
M=D-B*(C/A)
The B*(C/A) term will be very, very close to zero. You can probably get a good approximation from just D. Don't forget to exhale maximally when you take hydrostatic measurements. Typically in body density measurements it's done just to ensure a true density is calculated (a correction factor for intestinal gases is included, too), but for our purposes, you just need to be consistent, since we don't care about your true hydrostatic mass -- we're just using it as a correction factor.
As an aside, you will get an estimate of your body fat percentage. Typical underwater weighing measurement assume fat has a density of ca .9, and fat free mass has a density of ca 1.1. So your body fat percentage is (495/True density) - 450, or (457/True density) - 414.2, depending whom you trust. These are known as the Siri and Brozek equations. The disclaimers above about dead volume in lungs and the GI apply moreso here; body fat determination is extremely error-prone, especially in those <1 0 and>30% BF (most of us...).
posted by oxonium at 9:43 PM on April 22, 2006
individual variations in mass are likely due to abdominal fat deposits
Should read individual variations in density.
posted by oxonium at 9:52 PM on April 22, 2006
Should read individual variations in density.
posted by oxonium at 9:52 PM on April 22, 2006
I don't know the solution, but I admire the problem. Can you tell us why it's really important?
posted by Dub at 10:06 PM on April 22, 2006
posted by Dub at 10:06 PM on April 22, 2006
Solving this problem clearly requires decapitation.
Assumptions about head density, whether they involve assuming your head is the same density as the rest of you, or whatever else, seem to me to be an inaccurate way to go about this. I do like rolypolyman's idea, except that you don't know if your skull is average in weight or not (since you don't know if your skull is average in volume). We need head density data, measured by weighing heads.
Luckily, the decapitation has been done for you, and you can just make use of the data from other peoples' heads.
Here's what I suggest: read through some medical literature, and find out the mass of the average head, and the volume of the average head. This data has to be out there, right? This is the internet.
Divide to get the density of the average head, and then simply multiply by the volume of your head - the measuring of which has been amply covered in this thread.
Unless your head has considerably more or less fat content than most, I'm guessing this result should get you awfully close - definitely within 10 percent, maybe better. It's possible that you could even find data on the variance of head density, which would allow you to determine how probable it is that your estimate is accurate to whatever degree. I found this in a few minutes - it includes the neck, but it makes me think there's more out there.
posted by pinespree at 10:13 PM on April 22, 2006 [1 favorite]
Assumptions about head density, whether they involve assuming your head is the same density as the rest of you, or whatever else, seem to me to be an inaccurate way to go about this. I do like rolypolyman's idea, except that you don't know if your skull is average in weight or not (since you don't know if your skull is average in volume). We need head density data, measured by weighing heads.
Luckily, the decapitation has been done for you, and you can just make use of the data from other peoples' heads.
Here's what I suggest: read through some medical literature, and find out the mass of the average head, and the volume of the average head. This data has to be out there, right? This is the internet.
Divide to get the density of the average head, and then simply multiply by the volume of your head - the measuring of which has been amply covered in this thread.
Unless your head has considerably more or less fat content than most, I'm guessing this result should get you awfully close - definitely within 10 percent, maybe better. It's possible that you could even find data on the variance of head density, which would allow you to determine how probable it is that your estimate is accurate to whatever degree. I found this in a few minutes - it includes the neck, but it makes me think there's more out there.
posted by pinespree at 10:13 PM on April 22, 2006 [1 favorite]
The Internation Federation of Competitive Eating may be able to help. There was a kerfuffle in January about a burger-eating competition that invited contestants to plough through a giant burger that may or may not have weighed the same as David Hasselhoff's head. After contestants complained that the burger was probably much bigger than the Hoff's noggin, the organisers wrote a letter to Hasselhoff asking him to get his head weighed to settle the issue. According to the article:
"The weighing process will either employ volumetrics (submersion in water) or require Hasselhoff to lie on a table with his head extended over the edge onto a scale."
But if you're looking for a ball-park figure [from the same article], "according to the Department of Anatomy & Histology, University of Sydney, an adult human cadaver head cut off at vertebra C3, with no hair, weighs between 4.5 and 5 kg (between 9.9 and 10.23 pounds)".
posted by hot soup girl at 10:29 PM on April 22, 2006 [1 favorite]
"The weighing process will either employ volumetrics (submersion in water) or require Hasselhoff to lie on a table with his head extended over the edge onto a scale."
But if you're looking for a ball-park figure [from the same article], "according to the Department of Anatomy & Histology, University of Sydney, an adult human cadaver head cut off at vertebra C3, with no hair, weighs between 4.5 and 5 kg (between 9.9 and 10.23 pounds)".
posted by hot soup girl at 10:29 PM on April 22, 2006 [1 favorite]
Adds to list of favorite quotes: "Solving this problem clearly requires decapitation."
posted by IronLizard at 10:54 PM on April 22, 2006
posted by IronLizard at 10:54 PM on April 22, 2006
I just want to put in another vote for NOT cutting your head off. It will be difficult to cut your head off without losing a lot of the blood weight.
My recommendation: get a high-speed camera, and stand facing the camera with your back to a wall with carefully measured centimeter markings. Relax your neck muscles as much as is possible.
Have a friend throw a baseball as hard as he can at the side of your head.
Review the tape and apply a little physics: you'll be able to determine the speed of the baseball just before impact, the speed of your head after impact, how much momentum was transferred, and how quickly your head accelerated, and therefore how much mass your head has.
If you go this way please let me know.
posted by IvyMike at 11:01 PM on April 22, 2006 [2 favorites]
My recommendation: get a high-speed camera, and stand facing the camera with your back to a wall with carefully measured centimeter markings. Relax your neck muscles as much as is possible.
Have a friend throw a baseball as hard as he can at the side of your head.
Review the tape and apply a little physics: you'll be able to determine the speed of the baseball just before impact, the speed of your head after impact, how much momentum was transferred, and how quickly your head accelerated, and therefore how much mass your head has.
If you go this way please let me know.
posted by IvyMike at 11:01 PM on April 22, 2006 [2 favorites]
Cut off half your head, weigh it, and multiply the result by two?
posted by Pinback at 11:04 PM on April 22, 2006
posted by Pinback at 11:04 PM on April 22, 2006
I can't possibly be the only one humming that Phish song as I read this thread. I'd like to cut your head off / so I could weigh it / Whaddaya say...?
posted by wanderingmind at 11:06 PM on April 22, 2006
posted by wanderingmind at 11:06 PM on April 22, 2006
Best answer: Alright, here are three methods for you mammary16. The principles invoked involve neutral buoyancy and all rely on you being able to tell when your head is being 'supported' while being held upside down. Results will probably be less accurate than if you had just weighed your head lying down on a bathroom scale.
Method #1 (No trusted friend available, spring physics)
a) Tie yourself to a very stiff spring attached to a ceiling. Using a rope, lower your head into the water (dense saltwater preferred) until you no longer feel the weight of your head.
b) measure the displacement of the spring from its rest position (call it x). Calculate the Force the water applied to your head using this formula F = -kx. This is a linear relation, so you can calculate k, which is called the spring constant, by measuring the force of other objects hanging from the spring and then doing a linear interpolation.
Method #2 (Trusted Friend Heavier than you Available, Pulley Physics)
a) From above, except the rope should be connected by frictionless pulleys to your trusted friend standing on a scale, who raises and lowers you until, by hand signal, you let him/her know that you can no longer feel the weight of your head. The position of the pulleys is important, they need to be directly overhead both of you.
b) Your friend just needs to look down at the scale and see how much your head is subtracting from his/her true weight. Please remind your friend to pull you out of the water when this is done.
Method #3 (Bathroom Physics!)
As in Methods #1 and #2, but just have your friend dunk you in the water. I would use a mostly filled bathtub or toilet bowl.
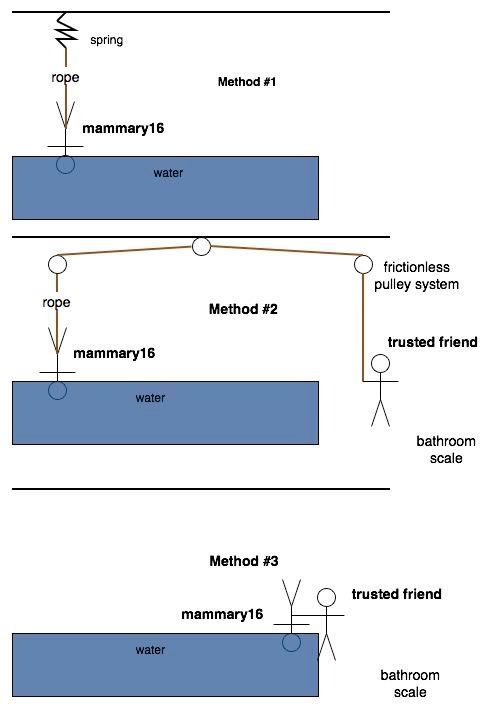
(Note: There WAS a bathroom scale in the original image, but OmniGraffle is being annoying, thanks to teece for helping me filter this into a JPG)
posted by onalark at 11:31 PM on April 22, 2006 [1 favorite]
Method #1 (No trusted friend available, spring physics)
a) Tie yourself to a very stiff spring attached to a ceiling. Using a rope, lower your head into the water (dense saltwater preferred) until you no longer feel the weight of your head.
b) measure the displacement of the spring from its rest position (call it x). Calculate the Force the water applied to your head using this formula F = -kx. This is a linear relation, so you can calculate k, which is called the spring constant, by measuring the force of other objects hanging from the spring and then doing a linear interpolation.
Method #2 (Trusted Friend Heavier than you Available, Pulley Physics)
a) From above, except the rope should be connected by frictionless pulleys to your trusted friend standing on a scale, who raises and lowers you until, by hand signal, you let him/her know that you can no longer feel the weight of your head. The position of the pulleys is important, they need to be directly overhead both of you.
b) Your friend just needs to look down at the scale and see how much your head is subtracting from his/her true weight. Please remind your friend to pull you out of the water when this is done.
Method #3 (Bathroom Physics!)
As in Methods #1 and #2, but just have your friend dunk you in the water. I would use a mostly filled bathtub or toilet bowl.

(Note: There WAS a bathroom scale in the original image, but OmniGraffle is being annoying, thanks to teece for helping me filter this into a JPG)
posted by onalark at 11:31 PM on April 22, 2006 [1 favorite]
lie on a table with your head extended beyond the edge, obtain one of those produce scales they use in the supermarket. Suspend it so the scoop is even with the table edge, put head in scoop, relax your neck.
posted by edgeways at 11:34 PM on April 22, 2006
posted by edgeways at 11:34 PM on April 22, 2006
Can I piggyback? I am interested in measuring the weight (not volume) of some mammary glands to which I am rather attached.
See Method #3 above. If you have a large basin sink this might do the trick. I'll leave the details to a non-physics geek who doesn't turn red in the face thinking of these things.
posted by onalark at 11:35 PM on April 22, 2006
See Method #3 above. If you have a large basin sink this might do the trick. I'll leave the details to a non-physics geek who doesn't turn red in the face thinking of these things.
posted by onalark at 11:35 PM on April 22, 2006
dersins wrote...
Yeah, I'm remembering my physics all wrong. I think the solution probably involves being hung by your heels from a spring-scale with your head in a vat of liquefied heads to achieve neutral head buoyancy, and then subtracting the reading on the spring-scale from the known weight of your entire body.
Flagged as fanstastic. Thank you, dersins.
posted by tkolar at 11:41 PM on April 22, 2006
Yeah, I'm remembering my physics all wrong. I think the solution probably involves being hung by your heels from a spring-scale with your head in a vat of liquefied heads to achieve neutral head buoyancy, and then subtracting the reading on the spring-scale from the known weight of your entire body.
Flagged as fanstastic. Thank you, dersins.
posted by tkolar at 11:41 PM on April 22, 2006
odinsdream: absolutely right, sorry. but substitute in "weight" for "mass" in the text and I still like the answer.
posted by oxonium at 11:57 PM on April 22, 2006
posted by oxonium at 11:57 PM on April 22, 2006
Still wouldn't work. Pretty much other than the liquified heads solution, everything that people have offered here will simply tell them something about the water that they're suspending themselves in.
For example:
Method #1 (No trusted friend available, spring physics)
a) Tie yourself to a very stiff spring attached to a ceiling. Using a rope, lower your head into the water (dense saltwater preferred) until you no longer feel the weight of your head.
b) measure the displacement of the spring from its rest position (call it x). Calculate the Force the water applied to your head using this formula F = -kx. This is a linear relation, so you can calculate k, which is called the spring constant, by measuring the force of other objects hanging from the spring and then doing a linear interpolation.
wouldn't work: What in fact occurs in this case is that you have two forces acting on the body; when you're at rest, they'll be in equilibrium, of course. There's the force due to the spring, and the buoyant force pushing you back up when you submerge your head. It's the unknown that you're trying to solve for--however, buoyant force is proportional to the mass of the liquid displaced, so once again, all you're doing is measuring the volume of your head, and not its mass.
posted by vernondalhart at 12:08 AM on April 23, 2006
For example:
Method #1 (No trusted friend available, spring physics)
a) Tie yourself to a very stiff spring attached to a ceiling. Using a rope, lower your head into the water (dense saltwater preferred) until you no longer feel the weight of your head.
b) measure the displacement of the spring from its rest position (call it x). Calculate the Force the water applied to your head using this formula F = -kx. This is a linear relation, so you can calculate k, which is called the spring constant, by measuring the force of other objects hanging from the spring and then doing a linear interpolation.
wouldn't work: What in fact occurs in this case is that you have two forces acting on the body; when you're at rest, they'll be in equilibrium, of course. There's the force due to the spring, and the buoyant force pushing you back up when you submerge your head. It's the unknown that you're trying to solve for--however, buoyant force is proportional to the mass of the liquid displaced, so once again, all you're doing is measuring the volume of your head, and not its mass.
posted by vernondalhart at 12:08 AM on April 23, 2006
Sorry, that should be proportional to weight, not mass.
posted by vernondalhart at 12:12 AM on April 23, 2006
posted by vernondalhart at 12:12 AM on April 23, 2006
when you're at rest, they'll be in equilibrium, of course
If they're at equilibrium, and you can no longer feel the weight of your head, that means the buoyant force is equal to the weight of your head, and it has been successfully subtracted from the weight of your body on the spring.
dersins still has the best answer by far, I just didn't have the stomach to draw a cartoon of liquified heads.
Oh, and the suggestion by pinespree of looking through the Internet to get the volume/weight relation is good as well. Taking a least-squares fit to the data would almost certainly get you within the realm of 5% error.
posted by onalark at 12:18 AM on April 23, 2006
If they're at equilibrium, and you can no longer feel the weight of your head, that means the buoyant force is equal to the weight of your head, and it has been successfully subtracted from the weight of your body on the spring.
dersins still has the best answer by far, I just didn't have the stomach to draw a cartoon of liquified heads.
Oh, and the suggestion by pinespree of looking through the Internet to get the volume/weight relation is good as well. Taking a least-squares fit to the data would almost certainly get you within the realm of 5% error.
posted by onalark at 12:18 AM on April 23, 2006
DR MASON'S method does not allow for the dense nature of the head, which contains much bone. A more accurate method is to float in the barrel, adjusting your lung volume to leave the head completely out of the water. While holding your breath, top up the barrel to the overflow and then submerge completely, collecting the displaced water, and measuring its volume. Climb out of the barrel, without further spillage, and then refill the barrel, measuring the volume needed. The floating volume of the body (the volume to keep the head up) can be calculated from the difference of the two volumes measured above. The weight of the head is the floating volume (in litres) less the body weight (in kilos).
Physics class eh? Don't ask mefi to do your homework... just google.
Using this method for breasts would be interesting.
posted by phrontist at 12:50 AM on April 23, 2006
Physics class eh? Don't ask mefi to do your homework... just google.
Using this method for breasts would be interesting.
posted by phrontist at 12:50 AM on April 23, 2006
Rhomboid: clord posits that the force required to pull an object up out of the water is proportional to the mass that is exposed. I posit that this is not the case.
Imagine someone floating, upright in a swimming pool, near the edge. You're standing on the edge of the pool. You reach down, hook your arms under their armpits, and try and lift them.
They feel much lighter than they would normally, right? Because they're floating in water, they have a buoyancy which is pushing them up, which helps you lift them.
Now imagine holding a person up like that, outside of the swimming pool. They feel much heavier -- in fact, they feel like their normal weight.
So now imagine that you're actually lifting a person out of the swimming pool. Where does the transition from 'feeling lighter' to 'normal weight' occur? Unless it occurs gradually (i.e. it occurs in proportion to the mass that is out of the water), you have to posit a transition point where their weight suddenly increases.
When does this happen? When they're half out of the water? The moment their big toe stops touching the water?
The idea of their weight suddenly increasing just doesn't jibe with any common experience. The only alternative is that their apparent weight must increase gradually as you lift them out of the water.
posted by chrismear at 4:44 AM on April 23, 2006
Imagine someone floating, upright in a swimming pool, near the edge. You're standing on the edge of the pool. You reach down, hook your arms under their armpits, and try and lift them.
They feel much lighter than they would normally, right? Because they're floating in water, they have a buoyancy which is pushing them up, which helps you lift them.
Now imagine holding a person up like that, outside of the swimming pool. They feel much heavier -- in fact, they feel like their normal weight.
So now imagine that you're actually lifting a person out of the swimming pool. Where does the transition from 'feeling lighter' to 'normal weight' occur? Unless it occurs gradually (i.e. it occurs in proportion to the mass that is out of the water), you have to posit a transition point where their weight suddenly increases.
When does this happen? When they're half out of the water? The moment their big toe stops touching the water?
The idea of their weight suddenly increasing just doesn't jibe with any common experience. The only alternative is that their apparent weight must increase gradually as you lift them out of the water.
posted by chrismear at 4:44 AM on April 23, 2006
I just realized that dersin's solution is only workable if we assume a uniform density for all of the heads involved. If the liquified heads were noticeably less dense than mammary16's, we'll end up believing his head is more massive than it actually is.
Of course, once we've decided to believe in uniform head density, we might as well skip the blender and just do weight and volume tests of each of the heads.
posted by tkolar at 6:00 AM on April 23, 2006
Of course, once we've decided to believe in uniform head density, we might as well skip the blender and just do weight and volume tests of each of the heads.
posted by tkolar at 6:00 AM on April 23, 2006
Shit, Rhomboid, sorry. I re-read what you wrote, and I now realise you're were actually making a different point to what I thought you were saying, and that I made a mistake in my post.
Of course the apparent weight changes gradually, but in changes with the volume that you've removed from the liquid, not the mass; which is what you've been saying all along.
posted by chrismear at 8:42 AM on April 23, 2006
Of course the apparent weight changes gradually, but in changes with the volume that you've removed from the liquid, not the mass; which is what you've been saying all along.
posted by chrismear at 8:42 AM on April 23, 2006
The idea of their weight suddenly increasing just doesn't jibe with any common experience.
Thank you, thank you, for not spelling this as "jive".
posted by Aknaton at 9:29 AM on April 23, 2006
Thank you, thank you, for not spelling this as "jive".
posted by Aknaton at 9:29 AM on April 23, 2006
You need three devices.
1. something to hold your body rigid below the neck; for example, wedge yourself between a large heavy object and a wall such that only your neck and head are free to move significantly.
2. something to measure acceleration. This can be done with a video camera. The faster the camera, the better the measurement will be.
3. something to measure the force of a light blow. A ball suspended on a rope will do.
Using the above objects, hit the ball with your head. The hight it swings to will indicate the force. Studying the video will indicate the acceleration. Because only your neck and head were involved, only their mass is relevent. mass = force / acceleration.
posted by treeshade at 9:49 AM on April 23, 2006
1. something to hold your body rigid below the neck; for example, wedge yourself between a large heavy object and a wall such that only your neck and head are free to move significantly.
2. something to measure acceleration. This can be done with a video camera. The faster the camera, the better the measurement will be.
3. something to measure the force of a light blow. A ball suspended on a rope will do.
Using the above objects, hit the ball with your head. The hight it swings to will indicate the force. Studying the video will indicate the acceleration. Because only your neck and head were involved, only their mass is relevent. mass = force / acceleration.
posted by treeshade at 9:49 AM on April 23, 2006
Lay on a seesaw, with your head on one side of the balance point and your body on the other (the neck is on the fulcrum). Add known weights to the head side until it equals the weight of the body. Then do math.
Total weight of person (t) = head weight (x) + body weight (b)
On the seesaw, the body weight is on one side and the added weights and head are on the other side; and when they're balanced, then b = weights added (w) + head (x)
Substituting in the original equation:
Total weight = head + added weights + head, or
t = 2x + w
Solving for x (head), 2x = t-w, or (t-w)/2 = x
QED
posted by mmw at 10:11 AM on April 23, 2006 [1 favorite]
Total weight of person (t) = head weight (x) + body weight (b)
On the seesaw, the body weight is on one side and the added weights and head are on the other side; and when they're balanced, then b = weights added (w) + head (x)
Substituting in the original equation:
Total weight = head + added weights + head, or
t = 2x + w
Solving for x (head), 2x = t-w, or (t-w)/2 = x
QED
posted by mmw at 10:11 AM on April 23, 2006 [1 favorite]
Just a thought, but all solutions that include using the entire body and it's mass as a starting point for determining the mass of the head must take into account the volume of air in the lungs when the body is floating. The mass/volume ratio for the torso is very different from that of the head, unless the head/sinuses actually contain the same ratio of air to solids and liquids as the torso/lungs. This I couldn't say.
posted by johngumbo at 11:20 AM on April 23, 2006
posted by johngumbo at 11:20 AM on April 23, 2006
I think I might have some helpful information...email is in my profile.
posted by mbd1mbd1 at 11:26 AM on April 23, 2006
posted by mbd1mbd1 at 11:26 AM on April 23, 2006
Lay on a seesaw, with your head on one side of the balance point and your body on the other (the neck is on the fulcrum).
This is actually an interesting approach, but needs some help to have a chance of being correct. In particular, you need to take the moment of inertia of the body into account -- it doesn't behave like a point mass. So you need to do some integrals. Other than that, it's my favorite solution in this thread.
Also, I just found the stumper problem for the next Calc II test I give.
posted by gleuschk at 11:26 AM on April 23, 2006 [1 favorite]
This is actually an interesting approach, but needs some help to have a chance of being correct. In particular, you need to take the moment of inertia of the body into account -- it doesn't behave like a point mass. So you need to do some integrals. Other than that, it's my favorite solution in this thread.
Also, I just found the stumper problem for the next Calc II test I give.
posted by gleuschk at 11:26 AM on April 23, 2006 [1 favorite]
Okay, go to a grocery store with a friend and both of you wander over to the produce section.
Lay down a 6'x2'x5" slab of something—I bet you could use a slab of super-firm foam. The point of the thing is that your body needs to be flat, fully supported and a few inches off of the ground. I supposed a picnic table would be perfect, although it'd be a lot higher than it needs to be.
So, you're lying on this slab/table, your whole body being supported by the thing. Now, skootch up a little so your head and neck are hanging off of the slab.
Now, take the metal chain-and-tray thing off of the hanging produce scale and tie a little cloth sling in it's place. Like a little head hammock. Your friend puts your head gently into the sling, such that when the scale is supporting the heads weight it is level with the rest of your body (neither higher nor lower than it would be if your head was lying on the slab/table).
Note weight on scale. (ex: 9 pounds)
Remove head.
Note weight again. (ex: 1 pound -- the weight of the sling)
Subtract latter from former.
(although this'll probably give you a little "neck weight")
posted by blueberry at 3:02 PM on April 23, 2006
Lay down a 6'x2'x5" slab of something—I bet you could use a slab of super-firm foam. The point of the thing is that your body needs to be flat, fully supported and a few inches off of the ground. I supposed a picnic table would be perfect, although it'd be a lot higher than it needs to be.
So, you're lying on this slab/table, your whole body being supported by the thing. Now, skootch up a little so your head and neck are hanging off of the slab.
o-< ---br>
_[[[[]]]]Now, take the metal chain-and-tray thing off of the hanging produce scale and tie a little cloth sling in it's place. Like a little head hammock. Your friend puts your head gently into the sling, such that when the scale is supporting the heads weight it is level with the rest of your body (neither higher nor lower than it would be if your head was lying on the slab/table).
|
^
U-< ---br>
_[[[[]]]]Note weight on scale. (ex: 9 pounds)
Remove head.
Note weight again. (ex: 1 pound -- the weight of the sling)
Subtract latter from former.
(although this'll probably give you a little "neck weight")
posted by blueberry at 3:02 PM on April 23, 2006
Oh man, those little stick-figure things looked fine in preview but totally didn't work when posted. Basically, the first one should look like a person lying on a mattress with his head sticking out off of one end.
The second pictograph should look like the same person but with his head now supported by a little "head hammock" (which is attached to a hanging scale).
posted by blueberry at 3:06 PM on April 23, 2006
The second pictograph should look like the same person but with his head now supported by a little "head hammock" (which is attached to a hanging scale).
posted by blueberry at 3:06 PM on April 23, 2006
This is actually an interesting approach, but needs some help to have a chance of being correct. In particular, you need to take the moment of inertia of the body into account -- it doesn't behave like a point mass. So you need to do some integrals. Other than that, it's my favorite solution in this thread.
Could you maybe solve this problem by making the body itself the seesaw? I'm imagining some bolts through the neck for the fulcrum, and then someone could just put weights right in the middle of mammary16's face until everything balances. Of course, he'd have to be very tense for this to work.
posted by kenko at 3:30 PM on April 23, 2006
Could you maybe solve this problem by making the body itself the seesaw? I'm imagining some bolts through the neck for the fulcrum, and then someone could just put weights right in the middle of mammary16's face until everything balances. Of course, he'd have to be very tense for this to work.
posted by kenko at 3:30 PM on April 23, 2006
Another option that has not been mentioned.
Find an appropriate black-hole. The goal is to find one that is as close to a point-source as possible. Now remember from physics that the force of gravity is proportional to distance from the source. Stand on a platform above the hole. Measure your weight when from a fixed distance from the black hole. Then move closer to the black hole by the hight of your body minus the height of your head. This will put the base of your skull where your feet were previously. Measure your weight again.
Since the gradient is so strong, there should be a significant difference between these two readings. Combined with perfect information about how much mass is in the black hole, it should be possible to determine the weight of the head mathematically.
posted by clord at 5:49 PM on April 23, 2006
Find an appropriate black-hole. The goal is to find one that is as close to a point-source as possible. Now remember from physics that the force of gravity is proportional to distance from the source. Stand on a platform above the hole. Measure your weight when from a fixed distance from the black hole. Then move closer to the black hole by the hight of your body minus the height of your head. This will put the base of your skull where your feet were previously. Measure your weight again.
Since the gradient is so strong, there should be a significant difference between these two readings. Combined with perfect information about how much mass is in the black hole, it should be possible to determine the weight of the head mathematically.
posted by clord at 5:49 PM on April 23, 2006
And so....did we find out why the poster wanted to know this?
posted by Jofus at 9:08 AM on April 25, 2006
posted by Jofus at 9:08 AM on April 25, 2006
I like mmw's solution but it is flawed as you need to be dealing with moments not just weights.
If we modified his equations to take account of how far from the fulcrum the head, body and extra weights are, then you have a chance of it working.
I disagree with gleuschk in that I would be tempted to model both the head and body as point masses acting through their respective centres of gravity.
So... lie on the seesaw so that it balances, draw a line across your body where it crosses the fulcrum (this is your CofG) now lie as per mmw's solution and calculate the moments to equal zero (equilibrium) when you and the extra weights balance.
posted by SpacemanRed at 1:12 AM on April 26, 2006 [1 favorite]
If we modified his equations to take account of how far from the fulcrum the head, body and extra weights are, then you have a chance of it working.
I disagree with gleuschk in that I would be tempted to model both the head and body as point masses acting through their respective centres of gravity.
So... lie on the seesaw so that it balances, draw a line across your body where it crosses the fulcrum (this is your CofG) now lie as per mmw's solution and calculate the moments to equal zero (equilibrium) when you and the extra weights balance.
posted by SpacemanRed at 1:12 AM on April 26, 2006 [1 favorite]
« Older Looking for more words like this: "Pull apart the... | How to repair a scratch on laminate flooring? Newer »
This thread is closed to new comments.
2. Fill with enough water to fully submerge your head.
3. Dunk head in water.
4. Have friend measure volume of water displaced in cubic centimeters. (Hope he can measure quickly.)
5. Unless my memory of high school physics is mistaken-- which is possible, given that it was 19 years ago-- that should be the mass of your head in grams.
posted by dersins at 5:50 PM on April 22, 2006