Lineweaver-burk woes.

February 15, 2006 8:32 AM

BioChemistryFilter: How do I read the vMax and Km off of a Lineweaver-burk plot?

This is probably so easy as to be obvious but having sat here all afternoon with lecture notes and biochem books i'm still none the wiser so... say i have a Lineweaver-burk plot that looks similar to this:


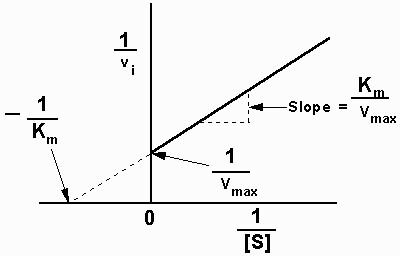
Assuming there are values along the x & y axis, how do i read the vMax and Km off of this plot. Is it as simple as Km being the "up" measurement on the "slope" and vMax being the "across" measurement (or vice-versa)? Or is there something more complex involved to get these values?

Also, if it is more complex, are there any websites available that can explain the Lineweaver-burk plot in simple, baby-like, steps?

Thanks for any help!

posted by tnai to Science & Nature (9 answers total)

Best answer: It's been a long time since I've done this, but just looking at the graph you provide, vMax is the reciprocal of the y-intercept, and once you have that, the product of the slope and vMax is the Km.

You might do well to take a quick review of algebra, slope, y-intercepts, and the equations that describe lines and how they behave. The point of the Lineweaver-Burke plot is that you can get these useful numbers out of it with linear estimations (i.e. your graph paper and a straightedge), and you don't have to deal with more complicated mathematics.
posted by ikkyu2 at 9:05 AM on February 15, 2006

See where the line crosses the y axis? Divide 1 by that number. The result of this division is your Vmax.

Do you know how to measure the slope of the line? Figure out the slope of the line, and multiply it by Vmax. The result of this multiplication is your Km.
posted by mr_roboto at 9:43 AM on February 15, 2006

What ikkyu2 said. Trust your graph. The slope is a ratio, so you can't just take "up" and "across" measurements and have them be the correct values for Km or Vmax.

1/(y-intercept) = Vmax

Slope/(y-intercept) = Km
posted by rxrfrx at 9:46 AM on February 15, 2006

The negative reciprocal of the x-axis is the Km. You can then confirm your findings by comparing them to the values obtained from the slope (Km/Vmax).
posted by LunaticFringe at 9:48 AM on February 15, 2006

Best answer: What everybody else said. To sum up:

1. On a Lineweaver-Burk plot the y-intercept, or value at which the line intersects the y axis, is the reciprocal of Vmax. (If you need an algebra refresher, the reciprocal of any number "n" is 1/n.) Therefore, to get Vmax you should divide 1 by the y-intercept of the graph. This is expressed algebraically as Vmax = 1/(y-intercept).
2. The X-intercept, or value at which the line intersects the x axis, is the negative reciprocal of Km. Therefore, to get Km you should divide -1 by the x-intercept of the graph. This is expressed algebraically as Km = -1/(x-intercept). Since you are dividing a negative number by another negative number, this will give you a positive value for Km.

As others have pointed out you can also find either Vmax or Km first, then determine the slope of the line and use slope = Km/Vmax to calculate the final missing value. This method is less straightforward but you should probably try to understand it as well.
posted by purplemonkie at 10:35 AM on February 15, 2006

Response by poster: that's excellent! Thanks for all the help, I really appreciate it.
Especially, thanks to purplemonkie for breaking it down to the simplest level that i can understand.
Cheers! Tnai...
posted by tnai at 11:22 AM on February 15, 2006

LB plots are pretty inaccurate where it counts (Km, VMax) because the reciprocal values are based on extrapolations from data that is actually on the far right of the graph. Modern enzyme kinetics will plot regular or log data and do curve or linear fits.

Where they come in really handy is at-a-glance recognition of ideal competitive and noncompetitive competition for the active site of a catalytic enzyme.

Basically, a competitive inhibitor of the enzyme will be out-competed by increasing substrate concentration. In this case, you will see a bunch of lines with different slopes all intersecting on the y-axis (1/Vmax). This is because CIs have no effect on the Vmax but cause a different Km to manifest.

A noncompetitive inhibitor of the enzyme cannot be outcompeted by increasing substrate concentration (because it is not on the active site but mucking about with the allosterics or cooperativity or something else). In this case, you will see a bunch of lines with different slopes all intersecting on the x-axis (-1/Km). This is because by "knocking out" the some portion of the enzyme you are changing the Vmax but not the Km of the unaffected enzyme.

In reality, when you test a real enzyme you don't see ideal CI or NCI but instead a bunch of lines with varying slopes intersecting at a point or area between the x- and y-axes, top-left. In some cases you can pretty "ping pong" kinetics where the lines zig zag back and forth.
posted by meehawl at 4:23 PM on February 15, 2006

meehawl: I always suspected that the reason they crammed L-B plots down the throats of biochem majors was to scare off the ones who can't think quantitatively. They're not good for much apart from problem sets.
posted by ikkyu2 at 8:20 PM on February 15, 2006

They're not good for much apart from problem sets.

Actually, during my first year as a biochem grad student one of my rotation projects was the characterization of a newly identified putative protein tyrosine phosphatase, and I was surprised to find that one of my first assignments was to construct M-M and L-B plots to see whether the Km and Vmax values fell within the range reported for known tyrosine phosphatases. But this lab's focus was the study of signaling networks, not enzyme kinetics -- so approximate values were fine for our purposes. I'm sure that bona fide enzyme kinetics labs determine Km/Vmax using more accurate methods. In any case, it was refreshing to see the infamous L-B being put to scientific use; I'd always just thought of it as an easy ten points.
posted by purplemonkie at 6:49 AM on February 16, 2006